Koordinatensysteme
Um Positionsberechnungen auf der Erde durchführen zu können, muss die Erdoberläche mathematisch beschrieben werden. Dies kann natürlich nur näherungsweise geschehen, da praktisch nicht jeder Punkt auf der Erde einbeziehbar ist – man spricht bei der Form der Erde auch vom Geoiden1. Die gängigste Variante diesen Geoiden zu approximieren ist dabei die Verwendung einer Ersatzform, im einfachsten Fall einer Kugel. Da die Erde aber nicht ganz rund ist, verwendet man stattdessen lieber einen Ellipsoiden, welcher einen (größeren) äquatorialen Radius a2, einen (kleineren) polaren Radius b3 sowie eine sog. Abflachung f4 besitzt, welche sich direkt aus den beiden Radien a und b ergibt: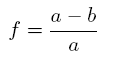
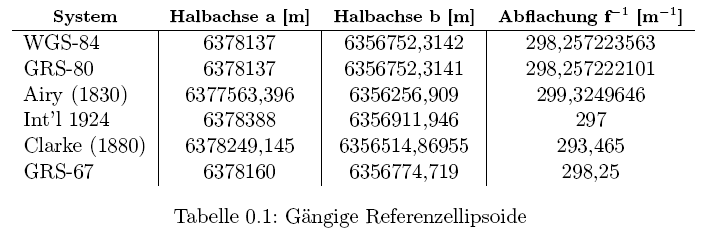
Die Grundlage für heutige GPS-Koordinaten ist der sog. WGS84-Ellipsoid, welcher bei globaler Betrachtung der genaueste ist. Andere Ellipsoide sind speziell für bestimmte Regionen des Geoiden (also der Erdoberfläche) angepaßt und bieten dort eine größere Genauigkeit, eignen sich jedoch nur bedingt für eine globale Anwendung. Für Großbritannien eignet sich beispielsweise der Airy-(1830)-Ellipsoid und ein Großteil von Europa wird gut mit dem International-1924-Ellipsoiden beschrieben. Weitere Ellipsoide sind in Tabelle 0.1 aufgeführt: Afrika: Clarke (1880), Südamerika: GRS-67, (Nord-)Amerika: NAD83 und Australien: GRS-80.
Generell kann jede Koordinate mit geeigneten Transformationsgleichungen auf einen beliebigen anderen Ellipsoiden umgerechnet werden, weshalb jeder Ellipsoid prinzipiell auch global anwendbar ist.
Die Koordinaten auf dem hier verwendeten WGS84-Ellipsoiden definieren eine Länge λ und eine Breite Φ, bezogen auf den Null-Meridian in Höhe Greenwich. Diese Definition von Ellipsoid und dazugehörigem Koordinatensystem wird auch als geodätisches Datum bezeichnet. Bei der Umrechnung von einem ins andere ist wichtig, dass nicht jedes geodätische Datum den gleichen Bezugsmeridian definiert. Die Höhe H definiert sich bei WGS84 als Abstand zum Ellipsoiden.
Die genaue Definition des Geoiden ist etwas abweichend, was hier jedoch zu weit führen würde. Siehe auch: http://www.goce-projektbuero.de/goce.html
semi major axis, [engl.] Halbachse a
semi minor axis, [engl.] Halbachse b
flattening, [engl.] Abflachung